《100 Java Mistakes and How to Avoid Them》笔记 2 | 隔叶黄莺 Yanbin Blog

2023-10-25 | 阅读(84)

继续阅读本书，编程语言处理数值都有可能出现问题，如溢出，整数的最大最小值不对称，Double.NaN 等。

由于 Java 学了 C，也用 0 开始的数字来表示 8 进制数，如 037, 010 分别是十进制的 31 和 8，这与现实不相符。因为如果你在纸上写下 037, 010, 几乎所有人(除了某些程序员)都会认为它们就是十进制的 37 和 10。但是 Java 表示 2 进制, 16 进制的方式没有问题的，如 0b10, 0x37。IntelliJ IDEA 看到使用 0 开头的 8 进制数会不建议那么使用. 8 进制数字的范围是 0~8, 所以 09 是错误的, 但是 Java 编译器似乎对此很陌生.

int a = 09;

IntelliJ IDEA 会提示 Integer number too large, 编译器提示说 java: ';' expected, 有点驴唇不对马嘴.

现在几乎没有必要使用 0 开始的 8 进制数的方式, 或许还有用的就是表示 Unix 下文件权限, 如

int fileMode = 0644

所以任何时候看到 0 开头的数字都必须仔细检视, 基本可以禁止使用这种方式

Java 中在数字溢出时不会报任何错误, 不同宽度类型的数值只取所需字节数, 如超过范围的 long 型赋值给 int 型, int 只取低位四个字节

long a = Integer.MAX_VALUE + 1;   // -2147483648  int 加 int 还是 int, 再赋值给 long 
long b = Integer.MAX_VALUE + 1L;  // 2147483648
int c = Integer.MAX_VALUE + 1;    // -2147483648
int d = (int)2147483648L;         // -2147483648

long a = Integer.MAX_VALUE + 1; // -2147483648 int 加 int 还是 int, 再赋值给 long

long b = Integer.MAX_VALUE + 1L; // 2147483648

int c = Integer.MAX_VALUE + 1; // -2147483648

int d = (int)2147483648L; // -2147483648

Integer.MAX_VALUE 是 2147483647, 这涉及到 Java 怎么表示正负数的问题, 正整数最大值最高是 0, 其余位是 1, 加 1 后, 全部变成 1, 而最高位是符号位, 所以变成了负数的另一个极端 -2147483648. 并且 Java 在内部是用补码表示的, 即正数为原码, 负数的话为反码 + 1 表示

再来一个以更小整形数 byte 为例

byte a = 0b00000000;
short b = 0b0000000010000000;
byte c = (byte) b;
System.out.println(a);
System.out.println(c);

byte a = 0b00000000;

short b = 0b0000000010000000;

byte c = (byte) b;

System.out.println(a);

System.out.println(c);

short 在转型为 8 位字节型时取低位 10000000, 因为最高位是 1, 所以是负数, 补码表示为 11111111, 就是 -(2^{^}7) = -128, 如果认为是原码表示那它就是 -0, 也算是 -128, 这样就整出个计算机内部的 -0 与 0 是不一样的东西了.

这个问题上说太多了, 虽然 Java 在数值溢出时得到的数字也是有规可循的, 但通常那个溢出的数字是没有意义的, 应选择足够宽的数值类型避免溢出.

还有个有意思的取负操作, 像某种整型数的最小值取负, 或 /-1 还是它本身, 如

Integer.MIN_VALUE/-1 == Integer.MIN_VALUE
-Integer.MIN_VALUE == Integer.MIN_VALUE
Math.abs(Integer.MIN_VALUE) // -2147483648, 绝对值还可能是一个负数

当看到 -2147483648/-1 == -2147483648 就不要太奇怪了, 因为 -2147483648 没有在整数范围内对应的 2147483648, 最大的正整数也就 2147483647, 它加上 1 溢出后就变回了 -2147483648.

对于数字膨胀快速的操作如乘，乘方, 或者求平均数等操作, 更容易产生溢出.

有什么好办法能避免溢出呢? 大约只能自己小心, 或者更宽的类型, 如果觉得 int 不够就选用 long, 或者用 BigInteger, 它不会溢出, 或者类似的 Math.addExact(x, y) 溢出时会报告异常。

无符号移位操作确实能解决除 2 的操作时避免溢出

int average = (1_000_000_000 + 2_000_000_000) / 2; // -647483648
int average = (1_000_000_000 + 2_000_000_000) >>> 1; // 1500000000

但谁会这么写代码呢？还得加上注释才能理解，真有这样的问题为何不直接用 long 型呢？

long average = (1_000_000_000L + 2_000_000_000) / 2; // 1500000000

或者用 BigInteger

int 运算溢出后再赋值给 long 型有一个实际的应用实例

void process(int seconds) {
    long microseconds = seconds * 1_000_000;
    useMicronsecons(microseconds);
}

void process(int seconds) {

long microseconds = seconds * 1_000_000;

useMicronsecons(microseconds);

}

设置时以秒为单位，最后应用时转换为微秒，但在 seoncds 超过 2147 秒(大约 35 分钟)，seconds * 1_000_000 溢出了, microseconds 可能得到一个负数，解决办法是让运算时就转换为 long 型

seconds * 1_000_000L

或者

long microseconds = TimeUnit.SECONDS.toMicros(seconds);

在处理财务数据时，更多考虑用 BigDecimal 替代 float 或 double, 这样更能避免运算中舍入后产生的精度问题，BigDecimal 有更大的精度。

float a = 1f / 3;
double b = 1d /3;
BigDecimal c = BigDecimal.valueOf(1).divide(BigDecimal.valueOf(3), MathContext.DECIMAL128);

float a = 1f / 3;

double b = 1d /3;

BigDecimal c = BigDecimal.valueOf(1).divide(BigDecimal.valueOf(3), MathContext.DECIMAL128);

以上三个值分别是

0.33333334
0.3333333333333333
0.3333333333333333333333333333333333

运算后转型赋值时常要小心，像 long a = aInt * 3000000, 它总是右边计算后得到一个 int 再赋给 long，同理

double half = aInt / 2;

也是在 aInt /2 后得到一个 int，再转型赋值为 double，所以在 aInt 为 2 或 3 时，half 都是一样的，所以必须让运算之前就转型再计算，写成

double half = 2 / 2.0;

我们可以对比一下这两个方法的字节码

void f1(int value) {
    double half = value / 2;
}

void f2(int value) {
    double half = value / 2.0;
}

void f1(int value) {

double half = value / 2;

}

void f2(int value) {

double half = value / 2.0;

}

字节码

  void f1(int);
    Code:
       0: iload_1
       1: iconst_2
       2: idiv
       3: i2d
       4: dstore_2
       5: return

  void f2(int);
    Code:
       0: iload_1
       1: i2d
       2: ldc2_w        #7                  // double 2.0d
       5: ddiv
       6: dstore_2
       7: return

void f1(int);

Code:

0: iload_1

1: iconst_2

2: idiv

3: i2d

4: dstore_2

5: return

void f2(int);

Code:

0: iload_1

1: i2d

2: ldc2_w #7 // double 2.0d

5: ddiv

6: dstore_2

7: return

我们可以看到 f1() 中是除(idiv) 完后结果再转型成 double(i2d), 而 f2 中是运算数先转型为 double(i2d), 再作除法(ddiv)

又回到 Integer.MIN_VALUE 的问题(Long.MIN_VALUE 也类似)。实际应用中在用 hashCode() 进行集群中选择节点时也可能出现问题，如

int node = Math.abs(obj.hashCode()) % NUMBER_OF_NODES;

当 obj.hashCode() 正好是 Integer.MIN_VALUE 时，算出的 node 就是一个负数

在 Java 15 及其后可用 Math.absExact 方法，Math.absExact(Integer.MIN_VALUE) 在结果为负数时会抛出 ArithmeticError 异常

Math.floorMod(obj.hashCode(), NUMBER_OF_NODES); // 永远返回一个正数

整数往浮点数转换时的精度丢失

int intVal = 1 << 28;
float floatVal = intVal; // 2.68435456E8
float floatValPlusOne = intVal + 1; // 2.68435456E8
System.out.println(floatVal == floatValPlusOne); // true

int intVal = 1 << 28;

float floatVal = intVal; // 2.68435456E8

float floatValPlusOne = intVal + 1; // 2.68435456E8

System.out.println(floatVal == floatValPlusOne); // true

造成 intVal 和 intVal + 1 相等，加了也是白加。原因是整数部分的精度丢失

int 最高位为符号位，其余 31 位是数值位
而 float 的总字节数也是 32 位，最高位也符号位，8 位表示指数，剩下的 23 位表示数值

所以 int 的 31 位数值位到了 float 后只取 23 位，因此加在最末尾的 1 就是白加，总是被舍去, 不光加 1 没用，加 10 也效。

找了两张图来揭示 Java 内部如何表示 float 和 double

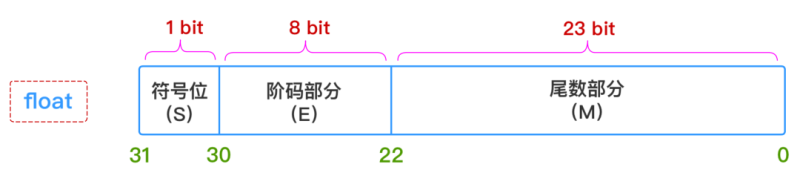
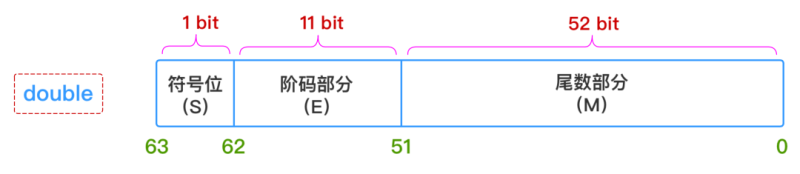看到 double 的尾数部分足够容纳 int 的全部，所以 int 转 double 不会有精度丢失的问题

这里又让我们再一次意识到用 BigDecimal 的必要性

在 long 型转 int 时，用 long a = (int)aLong; 会造成溢出问题，安全的方式可以用 Math.toIntExact(), 在存在溢出时会报告 ArithmeticException. Math 的更多 xxxExact() 方法还值得瞧瞧.

没用标识 L 的整数都是 int 型，包括带 0, 0b 或 0x 前缀的，如 0xFFFFFFFF, 要表示 long 也是用 0xFFFFFFFFL, 二进制，十六进制表示整数时同样要考虑到溢出

几个特殊的二进制表示边界值

byte a = (byte)0b1000_0001; // -127
byte b = (byte)0b1000_0000; // -128
byte c = (byte)0b1111_1111; // -128
byte d = (byte)0b0111_1111; // 127

byte a = (byte)0b1000_0001; // -127

byte b = (byte)0b1000_0000; // -128

byte c = (byte)0b1111_1111; // -128

byte d = (byte)0b0111_1111; // 127

x *= y 和 x = x + y 不尽相同，x *= y 相当于 x = (type_of_x)(x*y), 而 x = x * 1.2 时，如果 x 是整数时，x 会依据 1.2 的类型先转换为浮点数再乘以 1.2，得到的结果是一个 double，所以

char c = 'a';
c = c * 1.2; // c * 1.2 的 double 类型，无法赋值给 c

而 c *= 1.2 就是 't'

Byte.toUnsignedInt(getByte()); // Java 中想要用下无符号整形有点难

int min;

min = min * 3 / 2 与 min *= 3/2 是不一样的，后者是 min = min * (3/2), 即 min = min * 1。3/2 会在编译期计算为 1。当 min 是 4 时

min = min * 3/2 => min = 6

而 min *= 3/2 => min = 4

其实上面的问题归根结底就是要清楚是运算数转型后计算再转型赋值，还是计算后结果再转型。

还要就是 *= 运算时应把右端当成一个整体，比如 a -= b - c 是 a = a-(b-c), 相当于 a = a - b +c 而不是简单右移为 a = a - b - c

尽量不用 short 类型，所需数字一旦超过 32767 就产生溢出，用 int 对内存的影响微乎其微。

Java 处理位掩码时考虑用 BitSet. Java 中进行移位操作时请考虑到负数的情况，因为负数的最高位是符号位。

像整数在计算机中可能区分了 -0 与 +0，浮点数也有 -0.0 和 +0.0 的区别

double a = -1 * 0.0;
double b = 0.0;
System.out.println(a);
System.out.println(Double.doubleToLongBits(a));
System.out.println(b);
System.out.println(Double.doubleToLongBits(b));
System.out.println(a == b);
System.out.println(Objects.equals(a, b));

double a = -1 * 0.0;

double b = 0.0;

System.out.println(a);

System.out.println(Double.doubleToLongBits(a));

System.out.println(b);

System.out.println(Double.doubleToLongBits(b));

System.out.println(a == b);

System.out.println(Objects.equals(a, b));

输出为

-0.0
-9223372036854775808
0.0
0
true
false

虽然 -0.0 与 0.0 的基础类型是相等的，但装箱成 Double 后 Double(-0.0) 与 Double(0.0) 用 equals() 比较就不相等了，因为它们在内存中的表示形式却是不一样的。

NaN (Not-a-number) 也是很有意思的值，也是在 Java 中自己不等于自己的绝有的例子

System.out.println(Double.NaN == Double.NaN);   // false
System.out.println(Float.NaN == Float.NaN);     // false
System.out.println(Double.isNaN(Double.NaN));   // true
System.out.println(Double.isNaN(Float.NaN));    // true
System.out.println(Float.isNaN(Float.NaN));     // true

System.out.println(Double.NaN == Double.NaN); // false

System.out.println(Float.NaN == Float.NaN); // false

System.out.println(Double.isNaN(Double.NaN)); // true

System.out.println(Double.isNaN(Float.NaN)); // true

System.out.println(Float.isNaN(Float.NaN)); // true

当处理 Double 或 Float 类型，总是要问下自己是否会是 NaN, 如果有可能就要用 Double.isNaN(a) 或 Float.isNaN(a) 来判断或断言。

而且浮点数还有相应的正负无限数值，见

System.out.println(Double.POSITIVE_INFINITY);                           // 1.0/0.0 的表示，打印为 Infinity
System.out.println(Double.NEGATIVE_INFINITY);                           // -1.0/0.0 的表示，打印为  -Infinity
System.out.println(Double.POSITIVE_INFINITY==Double.POSITIVE_INFINITY); // true
System.out.println(Double.isInfinite(Double.POSITIVE_INFINITY));        // true

System.out.println(Double.POSITIVE_INFINITY); // 1.0/0.0 的表示，打印为 Infinity

System.out.println(Double.NEGATIVE_INFINITY); // -1.0/0.0 的表示，打印为 -Infinity

System.out.println(Double.POSITIVE_INFINITY==Double.POSITIVE_INFINITY); // true

System.out.println(Double.isInfinite(Double.POSITIVE_INFINITY)); // true

浮点数可表示正负范围中的值，Double.MAX_VALUE 是最大值，然而 Double.MIN_VALUE 却不是最小值

System.out.println(Double.MAX_VALUE);  // 1.7976931348623157E308
System.out.println(Double.MIN_VALUE);  // 4.9E-324

double a = -Double.MAX_VALUE;
System.out.println(a < Double.MIN_VALUE);  // true

System.out.println(Double.MAX_VALUE); // 1.7976931348623157E308

System.out.println(Double.MIN_VALUE); // 4.9E-324

double a = -Double.MAX_VALUE;

System.out.println(a < Double.MIN_VALUE); // true

当真要一个更理想的 Double 最小值，用 -Double.MAX_VALUE 会更合适些。或者用 Double.POSITIVE_INFINITY 和 Double.NEGATIVE_INFINITY 来取代相应的 Double.MAX_VALUE 和 Double.MIN_VALUE

System.out.println(Double.POSITIVE_INFINITY > Double.MAX_VALUE);    // true
System.out.println(Double.NEGATIVE_INFINITY < -Double.MAX_VALUE);   // true

1 2	System.out.println(Double.POSITIVE_INFINITY > Double.MAX_VALUE); // true System.out.println(Double.NEGATIVE_INFINITY < -Double.MAX_VALUE); // true

Float 同 Double 一样，也是这个路数，但 BigDecimal 就不存在 NaN 这个数。

本文链接 https://yanbin.blog/100-java-mistakes-and-how-to-avoid-them-notes-2/, 来自隔叶黄莺 Yanbin Blog

ddd on postgres in (?,?) 和 =any(?) 用法/性能对比好文章
Perry Conn on Java 9 前/后使用 JAXB (包括支持 javax.* 或 jakarta.*)Your writing has a way of making even the most complex topics accessib...
Yanbin on Windows 安装使用 GCC(mingw-w64)是的，像 Rust 和 dotnet core 一样，都可以支持 Cross compile. Rust 和 g++ 在 Linux 下编译...
MerrickZ on Windows 安装使用 GCC(mingw-w64)我记得G++/GCC都是支持交叉编译的，你可以在linux/macos下面编译出windows平台的二进制PE文件……
Jack on 从 Rust 官方文档理解 Ownership哈哈，年纪大了才会下垂