前面讲过的几种排序多是以排序逻辑来命名的，例如冒泡，选择和插入排序，以及其他如归并排序，当然还有觉得自己足够牛 X 快速排序命名。而本文要学习的排序算法叫做希尔排序是以其设计者 Donlad Shell 命令的排序算法，该算法在 1959 年公布，能以作者来命名的算法应该是很不错的，令设计者引以为傲的。最初写出冒泡和选择排序的就没以作者来命名，可能不好意说，更可能是公共思维。
那么什么是希尔排序呢？它实际上是插入排序算法的增强版本，又称递减增量排序算法。它对待排序列表进行间隔式分段插入 处理，从而总体上减少了元素的移动次数而达到性能的大大提升。那么理解希尔排序之前一定要先了解插入排序。那么为什么说希尔排序既是递减又是增量呢？
算法分析与理解
下面我们就来看希尔排序的基本思路，同时理解其中的递减，增量，插入这几个概念。希尔排序对列表按间隔跳跃分组，对每个分组采用插入排序，完后递减间隔数再分组插入排序，直到间隔数为 1 时即进行一个全列表插入排序。
看下面的演示图，间隔增量初始为 3，而后递减到 1，实际排序中初始增量是有讲究的，如果初始为 1 就是一个标标准准的插入排序。
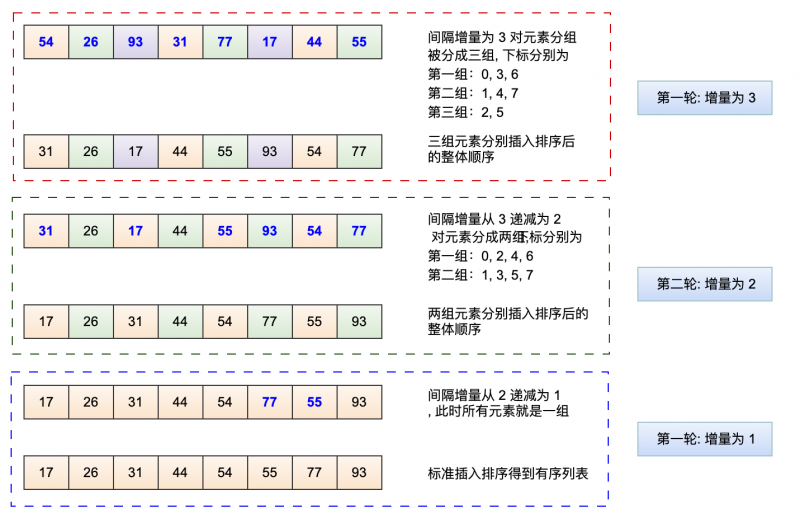从上图我们可以看到为什么叫做递减增量排序。为什么不是采用连续分组而是按增量的跳跃分组，因为跳跃的分组才能使得整个列表在排序过程中趋于有序，而连续元素分组的内部排序毫无意义。
参考代码实现
好了，有插入排序代码的基础加上以上的算法理解，我们可以尝试书写自己的实现
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
def shell_sort(items): length = len(items) gap = 3 # gap 可以择为 len(items) // 2 while gap > 0: # 递减增量 for group_start in range(0, gap): # 按增量跳跃分组 for index in range(group_start + gap, length, gap): # 对每一个分组是一个标准的插入排序 position = index current_value = items[index] while position > group_start and items[position - gap] > current_value: items[position] = items[position - gap] position -= gap items[position] = current_value gap -= 1 items = [54, 26, 93, 31, 77, 17, 44, 55] shell_sort(items) print(items) |
查看排序过程(或点击链接在新窗口中查看)
再看看书上是怎么写的，好像没什么分别。就是前面代码直接使用了 3 作为初始间隔，对于列表长度为 3 或更短的，好像有点不妥，怎么分，分不了，但也不犯错，最终就是一次标准插入排序。
希尔排序的时间复杂度
从循环上看，希尔排序的时间复杂度也是 O(n2), 如果在间隔(步长)选择上掌握好，最坏情况下达到 O(n3/2), 直至 O(n log2 n) 的复杂度，对，就是快速排序的速度。
间隔(步长) 的选择
Donald Shell 最初建议步长为 n/2, 已知最好的步长序列是由 Sedgewick 提出的(1, 5, 19, 41, 109, ...), 以下是摘自维基百科 希尔排序 词条中的
已知的最好步長序列是由Sedgewick提出的(1, 5, 19, 41, 109,...)，該序列的項來自 和 這兩個算式/lydia.sinapova/www/cmsc250/LN250_Weiss/L12-ShellSort.htm#increments。這項研究也表明“比較在希爾排序中是最主要的操作，而不是交換。”用這樣步長序列的希爾排序比插入排序要快，甚至在小數組中比快速排序和堆排序還快，但是在涉及大量數據時希爾排序還是比快速排序慢。
另一個在大數組中表現優異的步長序列是（斐波那契數列除去0和1將剩餘的數以黃金分割比的兩倍的冪進行運算得到的數列）：(1, 9, 34, 182, 836, 4025, 19001, 90358, 428481, 2034035, 9651787, 45806244, 217378076, 1031612713,…)[2]
与插入排序的速度对比
既然说希尔排序是插入排序的增强版，那么增强了多少了呢？下面进行一组对比测试，其中希尔排序的步长是 41
比较测试代码如下：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
def insertion_sort(alist): for index in range(1, len(alist)): current_value = alist[index] position = index while position > 0 and alist[position - 1] > current_value: alist[position] = alist[position - 1] position = position - 1 alist[position] = current_value def shell_sort(items): length = len(items) # gap = length // 2 gap = 41 while gap > 0: for group_start in range(0, gap): for index in range(group_start + gap, length, gap): position = index current_value = items[index] while position > group_start and items[position - gap] > current_value: items[position] = items[position - gap] position -= gap items[position] = current_value gap -= 1 from timeit import Timer import random t1 = Timer('insertion_sort(alist1)', 'from __main__ import insertion_sort', globals=globals()) t2 = Timer('shell_sort(alist2)', 'from __main__ import shell_sort', globals=globals()) length = 100000 times = 1 alist = list(range(length)) alist1 = list.copy(alist) alist2 = list.copy(alist) print(t1.timeit(number=times), t2.timeit(number=times)) alist = random.sample(list(range(length)), length) alist1 = list.copy(alist) alist2 = list.copy(alist) print(t1.timeit(number=times), t2.timeit(number=times)) |
从以下列表中看到希尔排序对无序列表排序的速度优于纯粹的插入排序。
| 排序耗时(秒) | 插入排序 | 希尔排序 |
| 1 K 有序列表 | 0.000249725 | 00.006600888 |
| 1 K 无序列表 | 0.053902998 | 0.009157253 |
| 10 K 有序列表 | 0.001805490 | 0.075122025 |
| 10 K 无序列表 | 5.513631449 | 0.22346067 |
| 100 K 有序列表 | 0.023105048 | 0.809362354 |
| 100 K 无序列表 | 564.843062358 | 14.482590992 |
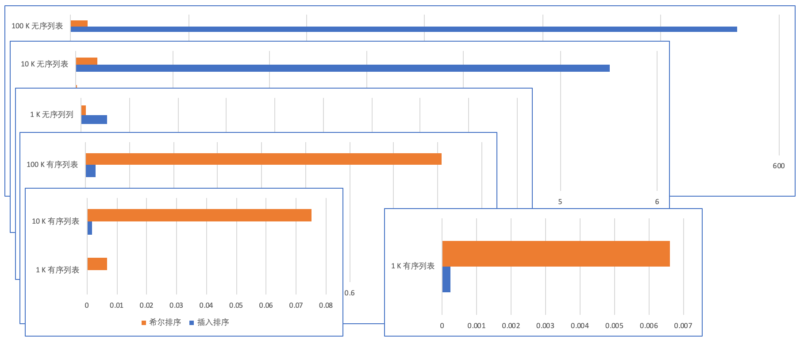
实际测试中希尔排序的步长对排序速度影响很大，如果用 n/2 作为步长，速度并不快，在我的测试中如果以 n/2 为步长，希尔排序时间比插入还慢。
本文链接 https://yanbin.blog/shell-sort-enhanced-insertion-sort/, 来自 隔叶黄莺 Yanbin Blog
[版权声明]
本文采用 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 进行许可。