插入排序算法解析
前面说过最原始的复杂度为 O(n2) 的冒泡和选择排序,也跳跃到了复杂度为 O(n log n) 的快速排序,现在又再看一个复杂度同样为 O(n2) 的插入排序。从排序名称结合代码我们理解了为什么叫做冒泡或是选择,快速排序自认高名,那么何以这又谓之插入排序呢?是怎么插入,从左边往右边插,还是从右边往左边插,这得搞清它的排序原理:
它在列表较低的一端维护一个有序的子列表(从最左端一个元素开始),并逐个将每个新元素(高端的)"插入"这个子列表。插入的时候遍历低端列表,找准位置插入便是,插入点后的元素需后移,当所有高端的元素插入完成了,整个列表就变得有序了。
整个排序操作示意图如下:
 好了,到此为止排序过程应该很清楚了,先不用看下面的代码,可以自己尝试写一段再进行对比。
好了,到此为止排序过程应该很清楚了,先不用看下面的代码,可以自己尝试写一段再进行对比。
我试了一段,如下:
排序后结果是对的,但中间结果有些跳跃,可从下面看到每一步的变化(或点击链接在窗口中查看)
执行中的大循环演化过程是对的
正确的插入排序代码应该是这样子的:
上面的插入排序代码插入时是在子列表中从后往前找,比当前元素大的后移,找到比当前元素小时,在该元素后插入当前元素。插入时也可以从左往右找位置,找到比当前元素小的时,在该位置前插入当前元素,剩下的子列表元素后移。交换操作的时间大约是移操作的 3 位,因为后都只需进行一次赋值。看下面的执行过程
或点击链接在新窗口中查看。
既然它的时间复杂度也是 O(n2),那么它在某些方面有什么好处没?稳定,比冒泡,选择要快,对比一下分别对十万有序和无序列表的排序时间。就不与快速排序比较了,本身就是不公平的。
比较代码:
排序有序/无序长度的列表的耗时
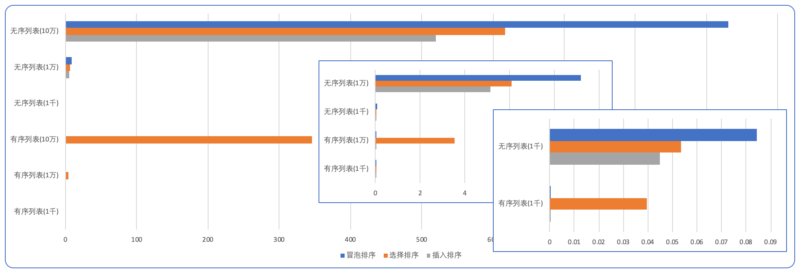 插入排序也是对有序列表友好的,免去了移动元素的消耗。插入排序比选择要快的很大一方面是由于交换比逐个移动列表元素要快,但估计对于链接的排序又是另一回事了。
更有序时,选择排序反而慢了,对于无序列表,冒泡效率低下,这三种排序方式相比而言,插入排序稍有些优势。对于同样是 O(n2) 复杂度的排序方式,减少元素的交换或移动的次数,或变交换为移动元素也能对效率有所提升。
插入排序也是对有序列表友好的,免去了移动元素的消耗。插入排序比选择要快的很大一方面是由于交换比逐个移动列表元素要快,但估计对于链接的排序又是另一回事了。
更有序时,选择排序反而慢了,对于无序列表,冒泡效率低下,这三种排序方式相比而言,插入排序稍有些优势。对于同样是 O(n2) 复杂度的排序方式,减少元素的交换或移动的次数,或变交换为移动元素也能对效率有所提升。
接下来会有一种对插入排序的增强版本,Shell 排序,对列表跳跃方式分段进行插入排序,最后一次完整插入排序,目的也是减少了元素的移动次数而得以优化。 永久链接 https://yanbin.blog/insertion-sort-how-to/, 来自 隔叶黄莺 Yanbin's Blog
[版权声明] 本文采用 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 进行许可。
本文采用 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 进行许可。
它在列表较低的一端维护一个有序的子列表(从最左端一个元素开始),并逐个将每个新元素(高端的)"插入"这个子列表。插入的时候遍历低端列表,找准位置插入便是,插入点后的元素需后移,当所有高端的元素插入完成了,整个列表就变得有序了。
整个排序操作示意图如下:
 好了,到此为止排序过程应该很清楚了,先不用看下面的代码,可以自己尝试写一段再进行对比。
好了,到此为止排序过程应该很清楚了,先不用看下面的代码,可以自己尝试写一段再进行对比。我试了一段,如下:
1items = [54, 26, 93, 17, 77, 31, 44, 55, 20]
2
3for i in range(1, len(items)):
4 for j in range(i):
5 if items[i] < items[j]:
6 items[i], items[j] = items[j], items[i]
7
8
9print(items) # [17, 20, 26, 31, 44, 54, 55, 77, 93]排序后结果是对的,但中间结果有些跳跃,可从下面看到每一步的变化(或点击链接在窗口中查看)
执行中的大循环演化过程是对的
如果要看每一步循环后的结果的话会有下面的中间状态:
- [54, 26, 93, 17, 77, 31, 44, 55, 20]
- [26, 54, 93, 17, 77, 31, 44, 55, 20]
- [26, 54, 93, 17, 77, 31, 44, 55, 20]
- [17, 26, 54, 93, 77, 31, 44, 55, 20]
- [17, 26, 54, 77, 93, 31, 44, 55, 20]
- [17, 26, 31, 54, 77, 93, 44, 55, 20]
- [17, 26, 31, 44, 54, 77, 93, 55, 20]
- [17, 26, 31, 44, 54, 55, 77, 93, 20]
- [17, 20, 26, 31, 44, 54, 55, 77, 93]
[26, 54, 93, 17, 77, 31, 44, 55, 20]插入 17 后,原本排好的 26 又跑到了 93 后面,插入 77 后 26 再一次回到了正确的位置上。也就是说插入结果后,插入点后方的元素并非整体后移,而且循环次数也较多。
[17, 54, 93, 26, 77, 31, 44, 55, 20]
[17, 26, 93, 54, 77, 31, 44, 55, 20]
正确的插入排序代码应该是这样子的:
1def insertion_sort(alist):
2 for index in range(1, len(alist)):
3 currentvalue = alist[index]
4 position = index
5
6 while position > 0 and alist[position-1] > currentvalue:
7 alist[position] = alist[position -1]
8 position = position -1
9
10
11 alist[position] = currentvalue
12
13
14items = [54, 26, 93, 17, 77, 31, 44, 55, 20]
15insertion_sort(items)上面的插入排序代码插入时是在子列表中从后往前找,比当前元素大的后移,找到比当前元素小时,在该元素后插入当前元素。插入时也可以从左往右找位置,找到比当前元素小的时,在该位置前插入当前元素,剩下的子列表元素后移。交换操作的时间大约是移操作的 3 位,因为后都只需进行一次赋值。看下面的执行过程
或点击链接在新窗口中查看。
既然它的时间复杂度也是 O(n2),那么它在某些方面有什么好处没?稳定,比冒泡,选择要快,对比一下分别对十万有序和无序列表的排序时间。就不与快速排序比较了,本身就是不公平的。
比较代码:
1def bubble_sort(items):
2 exchanges = True
3 for i in range(len(items)):
4 if not exchanges:
5 return
6 exchanges = False
7 for j in range(len(items) - i - 1):
8 if items[j] > items[j + 1]:
9 exchanges = True
10 items[j], items[j + 1] = items[j + 1], items[j]
11
12def selection_sort(items):
13 length = len(items)
14 for i in range(length):
15 for j in range(i + 1, length):
16 if items[i] > items[j]:
17 items[i], items[j] = items[j], items[i]
18
19
20def insertion_sort(items):
21 for index in range(1, len(items)):
22 current_value = items[index]
23 position = index
24
25 while position > 0 and items[position - 1] > current_value:
26 items[position] = items[position - 1]
27 position = position - 1
28
29 items[position] = current_value
30
31
32from timeit import Timer
33import random
34
35t1 = Timer('bubble_sort(alist1)', 'from __main__ import bubble_sort', globals=globals())
36t2 = Timer('selection_sort(alist2)', 'from __main__ import selection_sort', globals=globals())
37t3 = Timer('insertion_sort(alist3)', 'from __main__ import insertion_sort', globals=globals())
38
39length = 10000
40
41times = 1
42alist = list(range(length))
43alist1 = list.copy(alist)
44alist2 = list.copy(alist)
45alist3 = list.copy(alist)
46print(t1.timeit(number=times), t2.timeit(number=times), t3.timeit(number=times))
47
48alist = random.sample(list(range(length)), length)
49alist1 = list.copy(alist)
50alist2 = list.copy(alist)
51alist3 = list.copy(alist)
52print(t1.timeit(number=times), t2.timeit(number=times), t3.timeit(number=times))排序有序/无序长度的列表的耗时
| 排序耗时(秒) | 有序列表(1千) | 有序列表(1万) | 有序列表(10万) | 无序列表(1千) | 无序列表(1万) | 无序列表(10万) |
| 冒泡排序 | 0.000115519 | 0.000962132 | 0.010000855 | 0.084467821 | 9.189967045 | 930.12178294 |
| 选择排序 | 0.039573398 | 3.538418601 | 346.357997123 | 0.053535146 | 6.09890444 | 617.163237883 |
| 插入排序 | 0.000135626 | 0.00145926 | 0.017356704 | 0.044791698 | 5.156643332 | 519.60119013 |
 插入排序也是对有序列表友好的,免去了移动元素的消耗。插入排序比选择要快的很大一方面是由于交换比逐个移动列表元素要快,但估计对于链接的排序又是另一回事了。
更有序时,选择排序反而慢了,对于无序列表,冒泡效率低下,这三种排序方式相比而言,插入排序稍有些优势。对于同样是 O(n2) 复杂度的排序方式,减少元素的交换或移动的次数,或变交换为移动元素也能对效率有所提升。
插入排序也是对有序列表友好的,免去了移动元素的消耗。插入排序比选择要快的很大一方面是由于交换比逐个移动列表元素要快,但估计对于链接的排序又是另一回事了。
更有序时,选择排序反而慢了,对于无序列表,冒泡效率低下,这三种排序方式相比而言,插入排序稍有些优势。对于同样是 O(n2) 复杂度的排序方式,减少元素的交换或移动的次数,或变交换为移动元素也能对效率有所提升。接下来会有一种对插入排序的增强版本,Shell 排序,对列表跳跃方式分段进行插入排序,最后一次完整插入排序,目的也是减少了元素的移动次数而得以优化。 永久链接 https://yanbin.blog/insertion-sort-how-to/, 来自 隔叶黄莺 Yanbin's Blog
[版权声明]
 本文采用 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 进行许可。
本文采用 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 进行许可。