向量间距离/相似度及用 Python 进行计算
[latexpage]计算距离的目的也是为了确定两个向量的相似度，这里的向量可以是纯数学的数组，或者是一系列带有某些可量化特征值的物件。写作本文的原由是需要用 Numpy 计算两个实际对象的相似度，实现代码非常简单，因此更不能满足于此，借此机会多多了解下向量之间距离和相似度的概念，还回顾下一些相关的数学知识。
计算两个向量的相似度有许多的方法，如
本文主要关注到欧氏距离和余弦相似度这两个数值的求解上。
开始用 Python 来计算两个向量之间的距离
模和范，模范是两个容易混淆的概念，有时它们又是同一个意义，相应的有模式，范式。中文中模是指 modules, 范指的是 norm。在 Google 中搜索了有关向量的模与范之后反而更糊涂了，有说向量的模表示为 |v|, 范表示为 ||v||，向量的模表示意义上也就是绝对值，实际上单元素向量的模就是元素的绝对值 |(x)| = |x|
或说模长为范数，范数有 L0, L1, L∞ 和 Lp 范数
L0 范数: 向量中所有非零分量的个数, X=(x1,x2,..., xn), ||X||0 = X 中所有非零分量的个数，若 A = (0, 3, 6), ||A||0 = 2
L1 范数: 向量中每个分量的绝对值之和, \[||X||_1=|x_1|+|x_2|+...+|x_n|, ||X||=\sum_{i=1}^n|x_i|\]
L2 范数: 向量中每个分量平方总和再开二次方, \[||X||2 = \(\sqrt{|x_1|^2+|x_2|^2+|x_3|^2}\)= \sqrt{\sum_{i=1}^n|x_i|^2\], 由于每个分量都平方了，所以可省略每个分量上的绝对值操作
L∞ 范数: 向量中每个分量的绝对值的最大值, ||X||∞ = max(|X1|, |X2| ... |Xn|)
Lp 范数: 向量在每个分量绝对值的 p 次数总和, 再开 p 次方, L2 活范数是 Lp 的特例 \[||x||_p=\sqrt[p]{|x_1|^p+|x_2|^p+...+|x_n|^p}=\sqrt{\sum_{i=1}^n|x_i|^2}\]
我们通常所说的范数是指 L2 范数，我们要计算的欧氏距离(欧几里得距离)对应的就是 L2 范数。向量的范数相当于是一维或多维空间的原点(0,0...0) 到向量点间的距离，即
和前面输出的结果一样, np.linalg.norm() 默认计算的是 L2 范数, 相当于 np.linalg.norm(ord=2), 再来看它用来计算一个向量的范数
就是计算向量 (3,4) 到原点间的距离
点积的概念我们将在后面学习到
math.dist() 函数计算两点间距离
最简单的原来就在手边
计算公式
两个向量间的余弦值可以通过欧几里得点积公式求出：
a . b = ||a|| ||b|| cos θ
给定两个属性的向量，A 和 B，其余弦相似 θ 由点的向量长度给出，如下所示
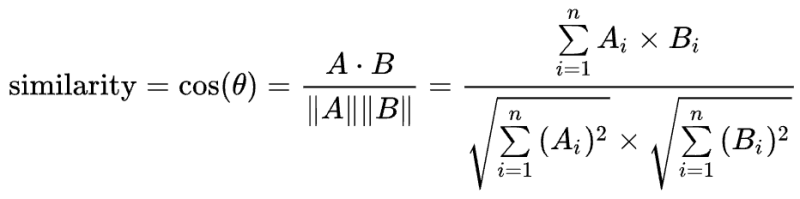这里的 Ai 和 Bi 分别代表向量 A 和 B 的各分量，通过前面的学习可知，||A|| 和 ||B|| 分别表示 A 和 B 的 L2 范数。
相似性值 -1 意味着两个向量指向截然相反，1 表示它们指向完全相同，0 通常表示它们是独立的。
关于向量的点积与叉积
点积(Dot product), 名称源自于点号 a .b, 读作 a dot b, 又称数量积或标量积，在欧几里得几何中，两个笛尔尔坐标向量的点积常称为内积(Inner product)
叉积(Cross product), 用符号
点积的定义如下
\[\vec{a} \cdot \vec{b} = \sum_{i=1}^n a_i b_i = a_1 b_1 + a_2 b_2 + \cdots + a_n b_n\]
精度上有一点误差
另外两种方式，使用 sklearn 或 torch 库
链接：
[版权声明]
本文采用 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 进行许可。
计算两个向量的相似度有许多的方法，如
- 欧氏距离(Euclidean Distance): 点间直线距离，数值越小越相似
- 夹角余弦(Cosine): 余弦相似度(Cosine Similarity)，计算两个向量之间的夹角，值在 -1 ～ 1 之间
- 曼哈顿距离(Manhattan Distance): 点间在坐标系上的绝对轴距总和
- 切比雪夫距离(Chebyshev Distance): 像国际象棋中的王从一格子到另一个格子间的距离
- 标准化欧氏距离(Standardized Euclidean distance): 先对各个分量进行标准化，再求欧氏距离
- 其他距离和相关系数，如马氏距离(Mahalanobis Distance), 兰氏距离(Lance Williams Distance); 皮尔逊相关系数(Pearson Correlation Coefficient), 杰卡德相似系数(Jaccard similarity coefficient)
本文主要关注到欧氏距离和余弦相似度这两个数值的求解上。
向量间的距离
当每个向量只有两个值时，两个向量表示的就是在平面坐标上的两个点，如 (x1, y1) 和 (x2, y2), 那么它们之间的距离公式可由勾股定理推导出来，即$$ \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$推广到三维空间的两个点，一个点可投影到另两个点所在的平面，经过多次勾股定理推算出相应的距离公式为
$$ d = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2} $$由此，任意维度中两个点间的距离就是 \[ D_{ij}^2 = \sum_{v=1}^n (X_{vi} - X_{vj})^2 \]
开始用 Python 来计算两个向量之间的距离
Python 集合推导形式
1import math
2
3def eucli_dist(A, B):
4 return math.sqrt(sum([(a-b)**2 for (a,b) in zip(A, B)]))
5
6print(eucli_dist((0,0), (3,4))) # 5.0
7print(eucli_dist((1,2,3), (3,5,8))) # 6.164414002968976利用 Numpy 两个向量间直接运算
1import numpy as np
2
3def eucli_dist(A, B):
4 return np.sqrt(sum(np.power((A-B), 2))) # 或者 np.sqrt(sum(np.square(A-B))
5
6print(eucli_dist(np.array([0,0]), np.array([3,4]))) # 5.0
7print(eucli_dist(np.array([1,2,3]), np.array([3,5,8]))) # 6.164414002968976Numpy 计算向量的范数(即距离)
说到向量的 模与 范, 就是一堆的线性代数的概念了, 当初学习线性代数和矩阵的时候可没想到如今还能用得上它们。Norm 源于拉丁语的 norma, 意为木匠用的三角规(Carpenter's square), 演变为英文就是 normal。模和范，模范是两个容易混淆的概念，有时它们又是同一个意义，相应的有模式，范式。中文中模是指 modules, 范指的是 norm。在 Google 中搜索了有关向量的模与范之后反而更糊涂了，有说向量的模表示为 |v|, 范表示为 ||v||，向量的模表示意义上也就是绝对值，实际上单元素向量的模就是元素的绝对值 |(x)| = |x|
或说模长为范数，范数有 L0, L1, L∞ 和 Lp 范数
L0 范数: 向量中所有非零分量的个数, X=(x1,x2,..., xn), ||X||0 = X 中所有非零分量的个数，若 A = (0, 3, 6), ||A||0 = 2
L1 范数: 向量中每个分量的绝对值之和, \[||X||_1=|x_1|+|x_2|+...+|x_n|, ||X||=\sum_{i=1}^n|x_i|\]
L2 范数: 向量中每个分量平方总和再开二次方, \[||X||2 = \(\sqrt{|x_1|^2+|x_2|^2+|x_3|^2}\)= \sqrt{\sum_{i=1}^n|x_i|^2\], 由于每个分量都平方了，所以可省略每个分量上的绝对值操作
L∞ 范数: 向量中每个分量的绝对值的最大值, ||X||∞ = max(|X1|, |X2| ... |Xn|)
Lp 范数: 向量在每个分量绝对值的 p 次数总和, 再开 p 次方, L2 活范数是 Lp 的特例 \[||x||_p=\sqrt[p]{|x_1|^p+|x_2|^p+...+|x_n|^p}=\sqrt{\sum_{i=1}^n|x_i|^2}\]
我们通常所说的范数是指 L2 范数，我们要计算的欧氏距离(欧几里得距离)对应的就是 L2 范数。向量的范数相当于是一维或多维空间的原点(0,0...0) 到向量点间的距离，即
\(||X||_2=\sqrt{|x_1-0|^2+|x_2-0|^2+|x_3-0|^2}\)那么任意两个点间的距离就是
\(||XY|| = \sqrt{|y_1-x_1|^2+|y_2-x_2|^2+|y_3-x_3|^2}\)在 Numpy 中用 np.linalg.norm() 函数求范数
1import numpy as np
2
3def eucli_dist(A, B):
4 return np.linalg.norm(A-B)
5
6print(eucli_dist(np.array([0,0]), np.array([3,4]))) # 5.0
7print(eucli_dist(np.array([1,2,3]), np.array([3,5,8]))) # 6.164414002968976linalg 即 linear algebra, 线性代数的意思和前面输出的结果一样, np.linalg.norm() 默认计算的是 L2 范数, 相当于 np.linalg.norm(ord=2), 再来看它用来计算一个向量的范数
1a = np.array([3,4])
2print(np.linalg.norm(a, ord=2)) # 5.0就是计算向量 (3,4) 到原点间的距离
通过点差及其转置的点积求得
1import numpy as np
2
3def eucli_dist(A, B):
4 temp = A - B
5 return np.sqrt(np.dot(temp.T, temp))
6
7print(eucli_dist(np.array([0,0]), np.array([3,4]))) # 5.0
8print(eucli_dist(np.array([1,2,3]), np.array([3,5,8]))) # 6.164414002968976点积的概念我们将在后面学习到
scipy 的 distance.euclidean() 函数
1from scipy.spatial import distance
2
3def eucli_dist(A, B):
4 return distance(A, B)
5
6print(eucli_dist((0,0), (3,4))) # 5.0
7print(eucli_dist((1,2,3), (3,5,8))) # 6.164414002968976math.dist() 函数计算两点间距离
1from math import dist
2
3def eucli_dist(A, B):
4 return dist(A, B)
5
6print(eucli_dist((0,0), (3,4))) # 5.0
7print(eucli_dist((1,2,3), (3,5,8))) # 6.164414002968976最简单的原来就在手边
余弦相似性计算
余弦相似性通过测量两个向量的夹角余弦值来度量它们之间的相似性，欧氏距离只管距离的绝对值, 余弦相似度只管方向。所有值在 -1 ~ 1 之间，指向相同方向时，即零度角，余弦值为 1， 90 度夹角余弦值为 0，反方向时相似度为 -1, 余弦相似度通常用于正空间，所以值在 0 ~ 1 之间。计算公式
两个向量间的余弦值可以通过欧几里得点积公式求出：
a . b = ||a|| ||b|| cos θ
给定两个属性的向量，A 和 B，其余弦相似 θ 由点的向量长度给出，如下所示
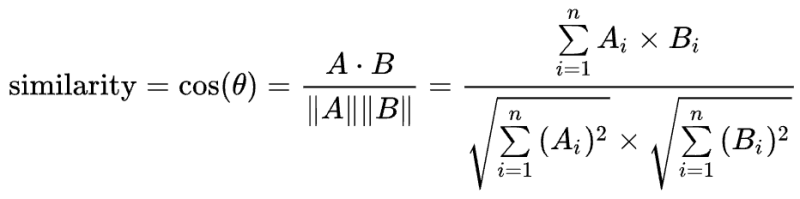这里的 Ai 和 Bi 分别代表向量 A 和 B 的各分量，通过前面的学习可知，||A|| 和 ||B|| 分别表示 A 和 B 的 L2 范数。相似性值 -1 意味着两个向量指向截然相反，1 表示它们指向完全相同，0 通常表示它们是独立的。
关于向量的点积与叉积
点积(Dot product), 名称源自于点号 a .b, 读作 a dot b, 又称数量积或标量积，在欧几里得几何中，两个笛尔尔坐标向量的点积常称为内积(Inner product)
叉积(Cross product), 用符号
X 表示，又称向量积，与点积不同的是，它的运行结果还是向量，相应的它也被称为外积(Outer product)点积的定义如下
\[\vec{a} \cdot \vec{b} = \sum_{i=1}^n a_i b_i = a_1 b_1 + a_2 b_2 + \cdots + a_n b_n\]
NumPy 计算余弦相似性
由上面的公式，使用 NumPy 就有了下面的计算余弦相似度代码1import numpy as np
2
3def cosine_similarity(A, B):
4 return np.dot(A, B) / (np.linalg.norm(A) * np.linalg.norm(B))
5
6x = np.array([1, 2, 3])
7y = np.array([3, 5, 8])
8
9print(cosine_similarity(x, y)) # 0.998906107238672用 scipy 计算余弦相似性
1from scipy import spatial
2
3def cosine_similarity(A, B):
4 return 1 - spatial.distance.cosine(A, B)
5
6x = (1, 2, 3)
7y = (3, 5, 8)
8
9print(cosine_similarity(x, y)) # 0.9989061072386719精度上有一点误差
另外两种方式，使用 sklearn 或 torch 库
使用 sklearn 的 cosine_similarity() 函数 计算余弦相似性
1import numpy as np
2from sklearn.metrics.pairwise import cosine_similarity as cs
3
4def cosine_similarity(A, B):
5 return cs(A.reshape(1, -1), B.reshape(1, -1))
6
7x = np.array([1, 2, 3])
8y = np.array([3, 5, 8])
9
10cos_sim = cosine_similarity(x.reshape(1, -1), y.reshape(1, -1))
11print(cos_sim[0][0]) # 0.998906107238672使用 touch 的 cosine_similarity() 函数
1import torch
2import torch.nn.functional as F
3
4x = torch.FloatTensor([1, 2, 3])
5y = torch.FloatTensor([3, 5, 8])
6
7cos_sim = F.cosine_similarity(x, y, dim=0)
8print(cos_sim.item()) # 0.9989060759544373链接：
- 计算向量间相似度的常用方法
- 向量 模 (module) 范数 (norm)
- 范数的概念
- 使用 NumPy 模块查找两点之间的欧几里得距离
- Python计算余弦相似性 (cosine similarity) 方法汇总
[版权声明]
本文采用 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 进行许可。