SciPy 最优化之最小化
[latexpage]
SciPy 是一个开源的算法库和数学工具包，可以处理最优化、线性代数、积分、插值、拟合、特殊函数、快速傅里叶变换、信号处理、图像处理、常微分方程求解器等。 它依赖于 NumPy, Pandas 也依赖了 NumPy。本文重点是体验它怎么处理最优化的问题。很多情形下通过 SciPy 的 optimize.minimize 方法寻求目标函数最小值的过程得到最优化的输入与输出。比如寻找二次元函数的根，求解线性/动态规则，金融行业的计算出最优投资组合的资产分配等。为什么 SciPy 没有 maximize 方法呢，因为没有必要，想要找到最大化的值，只要把目标函数的值取反，或者是模或绝对值的最小值。看到 minimize 方法名更让人觉得目标函数会有一个收敛值。
虽然 SciPy 对特定的问题有更直白的函数，如求根有 optimize.root, 线性规则 optimize.linprog(现不建议使用)，但各种优化基本都可以回归到 minimize 方法调用。minimize 方法的原型是
除了必须的目标函数和初始值，还有更多参数，像常用的约束(contraints) - 满足某些特定条件的最优化, 线程或非线性约束等; 求解方法(method) - Powell, Newton-CG 等
下面用 optimize.minimize 来求解一些问题
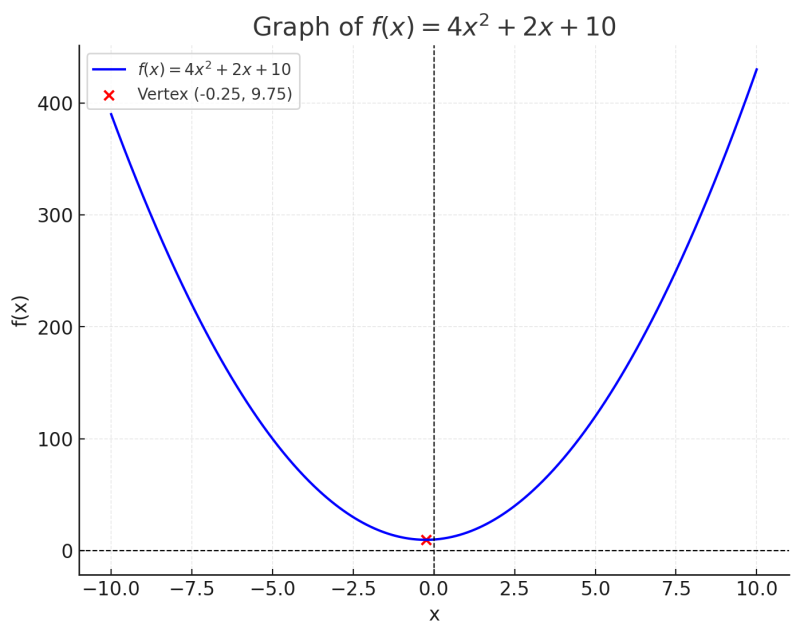根(顶点) 的 x 值是 [latex]x = -\frac{b}{2a} = -\frac{2}{8} = -0.25[/latex], 相应的 y 值是 9.75
现在来看用 minimize 怎么求解的，代码如下
x0 是猜测的初始值，minimize 通过迭代算出目标函数最小值的。
上面代码输出为
函数最小值为 9.75, x 为 -0.25，通过两次(nit) 迭代算出。
不同的初始值对结果也会影响
比如 x0 = np.array[10] 时， x=-0.2500001, f(x)=9.750000000000037
-1 和 10 是 -0.25 两边的值，所以 minimize 会向两边进行迭代，不同初始值会影响到迭代的次数。
我们可以输出它的迭代过程，用 callback 函数
输出为
很神奇，不知道它内部是怎么算定出 x=-0.25 时就是最小值的
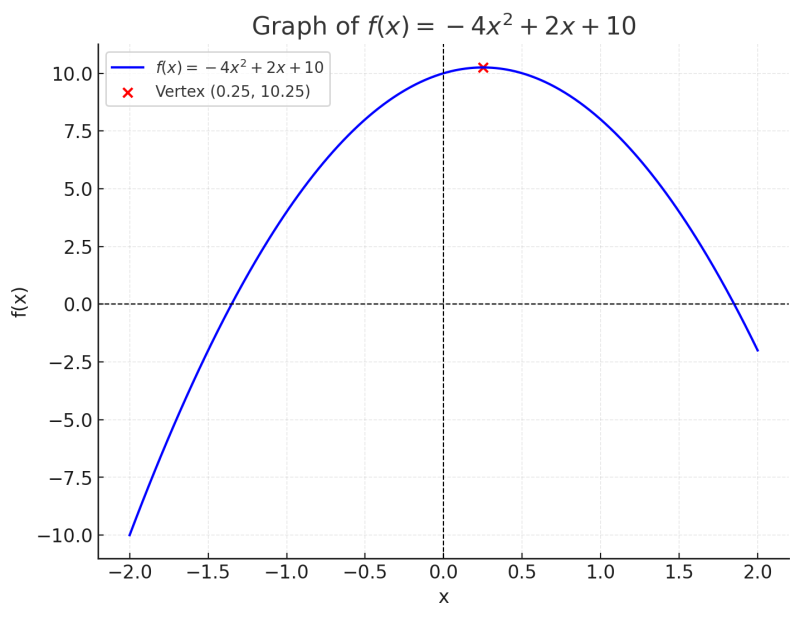
如果是一个下开口的二次函数 \( f(x) = -4x^2 + 2x + 10 \), 也试图求其最小值会如何呢？
输出结果
迭代一次就马上止住，给出答案为没有最小值。但只要改造一下目标函数, 即取反
这样就能算出它 x= 0.25 时最大值为 10.25，因为向下开口图形的顶点为最大值，取反则为最小值。
我们知道直线没有最小最大值，用 SciPy 试下求函数 \(f(x) = 4x + 10\) 的最小值
果然，结局是
现在是看图索骥了，就是想要知道 x, y 分别为多少时函数最小。把这个图形看成是一个地势高低图的话，就是在寻找畦地
输出为
如果预设 x0 = np.array([0,0]), 结果就是
初始预计值还是要有所讲究
分别得到两组结果
补上它的平面图
optimize.minimize 还可以实现曲线拟合问题，比如说找到相近的变化趋势，指纹/人脸检测等，当然这方面有更专业的工具箱
什么是背包问题:
有 n 种物品，物品 j 的重量和价值分别为 [latex]w_{j}[/latex] 和 [latex]v_{j}[/latex]，如果背包的最大容量限制是 m ，怎么样选择放入背包的物品以使得背包的总价值最大？
它是一个组合优化问题，设 [latex]x_{j}[/latex] 表示装入背包的第 j 个物品的数量, 那么目标函数和约束条件是：
解出问题后，结果为
这个问题还可以更复杂一些，比如说同一件物品可以拿多个进行组合。
链接：1. 最优化学习笔记 永久链接 https://yanbin.blog/scipy-optimize-minimize/, 来自 隔叶黄莺 Yanbin's Blog
[版权声明]
本文采用 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 进行许可。
SciPy 是一个开源的算法库和数学工具包，可以处理最优化、线性代数、积分、插值、拟合、特殊函数、快速傅里叶变换、信号处理、图像处理、常微分方程求解器等。 它依赖于 NumPy, Pandas 也依赖了 NumPy。本文重点是体验它怎么处理最优化的问题。很多情形下通过 SciPy 的 optimize.minimize 方法寻求目标函数最小值的过程得到最优化的输入与输出。比如寻找二次元函数的根，求解线性/动态规则，金融行业的计算出最优投资组合的资产分配等。为什么 SciPy 没有 maximize 方法呢，因为没有必要，想要找到最大化的值，只要把目标函数的值取反，或者是模或绝对值的最小值。看到 minimize 方法名更让人觉得目标函数会有一个收敛值。
虽然 SciPy 对特定的问题有更直白的函数，如求根有 optimize.root, 线性规则 optimize.linprog(现不建议使用)，但各种优化基本都可以回归到 minimize 方法调用。minimize 方法的原型是
1def minimize(fun, x0, args=(), method=None, jac=None, hess=None,
2 hessp=None, bounds=None, constraints=(), tol=None,
3 callback=None, options=None):除了必须的目标函数和初始值，还有更多参数，像常用的约束(contraints) - 满足某些特定条件的最优化, 线程或非线性约束等; 求解方法(method) - Powell, Newton-CG 等
下面用 optimize.minimize 来求解一些问题
求一元二次函数的最小值(根)
函数定义为 [latex]f(x) = 4x^2 + 2x + 10[/latex], 画出它的函数曲线如下
根(顶点) 的 x 值是 [latex]x = -\frac{b}{2a} = -\frac{2}{8} = -0.25[/latex], 相应的 y 值是 9.75现在来看用 minimize 怎么求解的，代码如下
1import scipy.optimize as opt
2import numpy as np
3
4def objective(x):
5 return 4*(x**2)+2*x+10
6
7x0 = np.array([-1])
8result = opt.minimize(objective, x0)
9
10print(result.x) # 目标函数最小值时输入 x
11print(result.fun) # 目标函数最小值
12print(result) # 迭代结果x0 是猜测的初始值，minimize 通过迭代算出目标函数最小值的。
上面代码输出为
1[-0.25]
29.75
3 message: Optimization terminated successfully.
4 success: True
5 status: 0
6 fun: 9.75
7 x: [-2.500e-01]
8 nit: 2
9 jac: [ 0.000e+00]
10 hess_inv: [[ 1.250e-01]]
11 nfev: 6
12 njev: 3函数最小值为 9.75, x 为 -0.25，通过两次(nit) 迭代算出。
不同的初始值对结果也会影响
比如 x0 = np.array[10] 时， x=-0.2500001, f(x)=9.750000000000037
-1 和 10 是 -0.25 两边的值，所以 minimize 会向两边进行迭代，不同初始值会影响到迭代的次数。
我们可以输出它的迭代过程，用 callback 函数
1def callback(xk):
2 print(f"Iteration: {callback.iter}, x = {xk}, y = {objective(xk)}")
3 callback.iter += 1
4
5callback.iter = 0
6
7x0 = np.array([100])
8result = opt.minimize(objective, x0, callback=callback)输出为
1Iteration: 0, x = [78.79], y = [24999.0364]
2Iteration: 1, x = [30.19728879], y = [3717.89957945]
3Iteration: 2, x = [-0.24999419], y = [9.75]
4Iteration: 3, x = [-0.25], y = [9.75]很神奇，不知道它内部是怎么算定出 x=-0.25 时就是最小值的
如果是一个下开口的二次函数 \( f(x) = -4x^2 + 2x + 10 \), 也试图求其最小值会如何呢？
1def objective(x):
2 return -4*(x**2)+2*x+10
3
4x0 = np.array([10])
5result = opt.minimize(objective, x0)
6print(result)输出结果
1 message: Desired error not necessarily achieved due to precision loss.
2 success: False
3 status: 2
4 fun: -4359650.2304
5 x: [ 1.044e+03]
6 nit: 1
7 jac: [-8.352e+03]
8 hess_inv: [[-1.250e-01]]
9 nfev: 236
10 njev: 112迭代一次就马上止住，给出答案为没有最小值。但只要改造一下目标函数, 即取反
1def objective(x):
2 return -(-4*(x**2)+2*x+10)这样就能算出它 x= 0.25 时最大值为 10.25，因为向下开口图形的顶点为最大值，取反则为最小值。
我们知道直线没有最小最大值，用 SciPy 试下求函数 \(f(x) = 4x + 10\) 的最小值
1def objective(x):
2 return 4 * x + 10
3
4x0 = np.array([10])
5result = opt.minimize(objective, x0)果然，结局是
message: Desired error not necessarily achieved due to precision loss.
success: False
求立体空间中的最小值
如果是一个二元的函数 [latex]f(x, y) = 4x^2 + 2y^2 + 10[/latex], 我们先画出它的图形来
现在是看图索骥了，就是想要知道 x, y 分别为多少时函数最小。把这个图形看成是一个地势高低图的话，就是在寻找畦地 1def objective(x_arr):
2 x, y = x_arr
3 return 4*(x**2) + 2*(y**2) + 10
4
5x0 = np.array([-10, -10])
6result = opt.minimize(objective, x0)
7
8np.set_printoptions(suppress=True) # 数值不以科学计数法输出
9print(result.x)
10print(result.fun)输出为
[-0.00000003 -0.00000005]去除误差，答案是正确的，也就是在 x=0, y=0，函数 f(x,y) 最小为 10.
10.000000000000009
如果预设 x0 = np.array([0,0]), 结果就是
1[0. 0.]
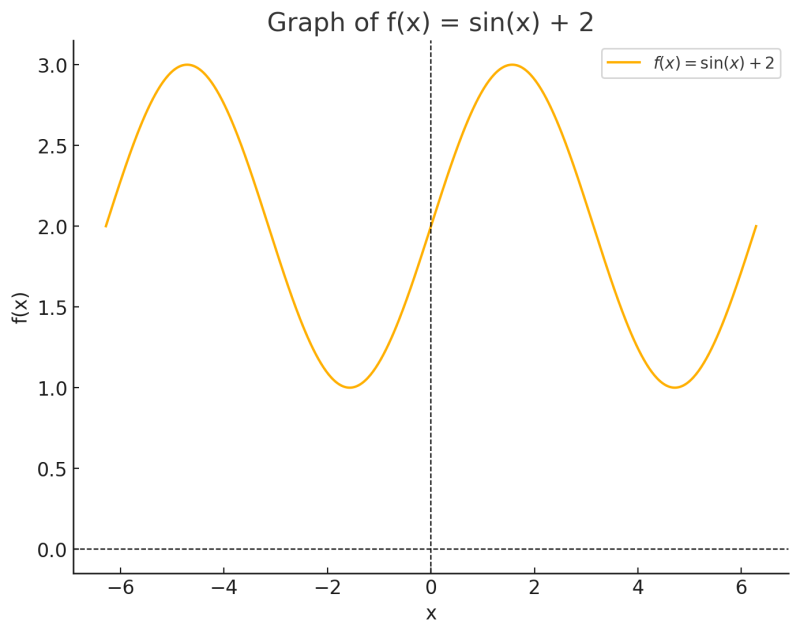
210.0求正弦函数的最小值
正弦函数[latex]f(x)=sin(x)+2[/latex] 是一个周期波，它有无数的波峰和波谷。我们的目的就是要找到猜测试值附近的波谷所在。上代码 1np.set_printoptions(suppress=True)
2
3def objective(x):
4 return np.sin(x) + 2
5
6x0 = np.array([0])
7result = opt.minimize(objective, x0)
8print(result.x)
9print(result.fun)
10
11print('---')
12
13x0 = np.array([5])
14result = opt.minimize(objective, x0)
15print(result.x)
16print(result.fun)分别得到两组结果
[-1.57079633]最小值都是一样的，所以都找到了各自猜测值附近的波谷位置
1.0
---
[4.71238898]
1.0
补上它的平面图
optimize.minimize 还可以实现曲线拟合问题，比如说找到相近的变化趋势，指纹/人脸检测等，当然这方面有更专业的工具箱关于背包问题
背包问题是一个整数的线性规划，scipy.optimize.linprog 可用来解决线性规划，但不适于整数的线性规划，因为背包中能装的物品数量是自然数。更适于解决整数的线程规划应该是 Pulp(PuLP is an linear and mixed integer programming modeler) 或 Pyomo. 什么是背包问题:
有 n 种物品，物品 j 的重量和价值分别为 [latex]w_{j}[/latex] 和 [latex]v_{j}[/latex]，如果背包的最大容量限制是 m ，怎么样选择放入背包的物品以使得背包的总价值最大？
它是一个组合优化问题，设 [latex]x_{j}[/latex] 表示装入背包的第 j 个物品的数量, 那么目标函数和约束条件是：
目标函数：[latex]max\sum_{j=1}^{n}v_{j}x_{j}[/latex] 约束条件: [latex]\begin{cases}\sum_{j=1}^n w_j x_j \leq b \\x_j \in \mathbb{N}\end{cases}[/latex]下面是具体问题的求解
1from pulp import LpMaximize, LpProblem, LpVariable, lpSum, PULP_CBC_CMD
2
3weight_values = [(2, 3), (3, 4), (4, 5), (5, 6)] # 每个物品重量及价值
4capacity = 5 # 背包的最大承重
5
6problem = LpProblem(name="knapsack-problem", sense=LpMaximize) # 目标函数最大化
7
8# 决策, 1 为选择
9x = [LpVariable(f"x{i}", cat="Binary") for i in range(len(weight_values))]
10
11# 目标与约束
12problem.objective = lpSum(v[1] * x[i] for i, v in enumerate(weight_values))
13problem.addConstraint(lpSum(v[0] * x[i] for i, v in enumerate(weight_values)) <= capacity)
14
15status = problem.solve(PULP_CBC_CMD(msg=False))
16
17print("Selected items:")
18for i, v in enumerate(weight_values):
19 if x[i].value() == 1:
20 print(f" - Item {i + 1} (weight={v[0]}, value={v[1]})")
21
22print("Total value: %d" % problem.objective.value())解出问题后，结果为
Selected items:最后包的总重为: 5
- Item 1 (weight=2, value=3)
- Item 2 (weight=3, value=4)
Total value: 7
这个问题还可以更复杂一些，比如说同一件物品可以拿多个进行组合。
链接：1. 最优化学习笔记 永久链接 https://yanbin.blog/scipy-optimize-minimize/, 来自 隔叶黄莺 Yanbin's Blog
[版权声明]
本文采用 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 进行许可。