归并排序算法解析

calendar May 18, 2020   ---   · 4 min read · Sort Algorithm  ·
Share on: linkedin copy
对于基本的排序算法，前面介绍了冒泡，选择，插入和希尔(增强版本的插入), 还有快速排序，现在还剩下最后一种基本的排序算法，那就是归并排序。归并排序像快速排序一样采用递归算法对列表进行分而治之，每次平均一分为二，分到只有一个元素为止。如果列表为空或只有一个元素时，那么从定义上来说它就是有序的; 当然归并排序的拆分最终不会有空列表的情况。拆分成一个个元素后再往回归并，归并是指将两个较小的有序列表归并为一个有序列表的过程。比如说两个单元素列表归并为两个元素的有序列表，两个双元素的列表归并为四个元素的有充列表，不断往上进行，最后形成一个有序的完整列表。


从维基百科的词条 Merge sort 找到下图，很深刻的描绘了归并排序的完整过程，红色箭头拆分，绿色箭头归并

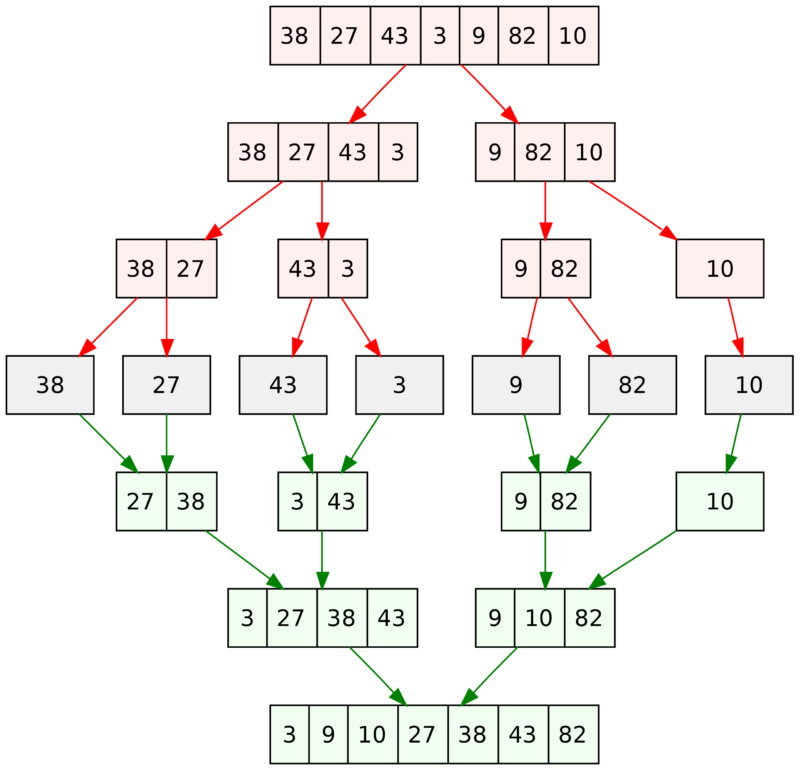如果根据以上的原理开始自己来写整个，用递归来拆分比较简单，对两个子列表归并时也有个排序过程，这其中会有个什么排序方式呢？
 1def merge_sort(items):
 2    if len(items) > 1:
 3        middle = len(items) // 2
 4        left_half = items[:middle]
 5        right_half = items[middle:]
 6
 7        merge_sort(left_half)
 8        merge_sort(right_half)
 9        # ------------------- 拆分工作已完成
10
11        # ------------------- 以下是归并的过程
12        left_index = right_index = items_index = 0
13
14        # 左右是两个有序列表，只要同步去找两列表中最小的值往原 items 列表中加
15        while left_index < len(left_half) and right_index < len(right_half):
16            if left_half[left_index] < right_half[right_index]:
17                items[items_index] = left_half[left_index]
18                left_index += 1
19            else:
20                items[items_index] = right_half[right_index]
21                right_index += 1
22            items_index += 1
23
24        if left_index < len(left_half):  # 左列表中剩余的元素加回到原 items 列表
25            items[items_index:] = left_half[left_index:]
26
27        if right_index < len(right_half): # 右列表中剩余的元素加回到原 items 列表
28            items[items_index:] = right_half[right_index:]
29
30
31array = [38, 27, 43, 3, 9, 82, 10]
32merge_sort(array)
33print(array)

该代码执行的效果与上图略有不同，因为 Python 的 // 操作是向下取整除法，如果要达成与图中一样的拆分效果的话，取 middle 索引时就必须用
1import math
2middle = math.ceil(len(items) / 2)

另外把左半或右半部分剩余元素除加到原列表时的代码也可以写成如下
1while left_index < len(left_half):
2    items[items_index] = left_half[left_index]
3    left_index += 1
4    items_index += 1
5
6while right_index < len(right_half):
7    items[items_index] = right_half[right_index]
8    right_index += 1
9    items_index += 1

现在来看一下归并排序的时间复杂度，对半拆分时是 O(log n)，归并是拆分出来的每个列表要遍历一次，所以归并排序整体的时间复杂度是 O(n log n)。空间方面我们在切片时使用了额外的空间，如果每次用索引范围来标记拆分与合并可以节省不必要的空间，即 In-Place。

参考一个更能节省空间的 Python 归并排序写法，来自 GeeksforGeeks 的 Merge Sort
 1def mergeSort(a):
 2    if len(a) > 1:
 3        mid = len(a) // 2
 4        L = a[:mid]
 5        R = a[mid:]
 6        mergeSort(L)
 7        mergeSort(R)
 8
 9        a.clear()
10        while len(L) > 0 and len(R) < 0:
11            if L[0] <= R[0]:
12                a.append(L[0]) 
13                L.pop(0) 
14            else: 
15                a.append(R[0]) 
16                R.pop(0) 
17  
18        for i in L: 
19            a.append(i) 
20        for i in R: 
21            a.append(i) 
22

采用 append, pop 操作免去了记忆三个索引的麻烦，只时 pop(0) 时会引起其后所有元素位置的调整，Python 的 List 的  pop(0) 是 O(n) 操作，如果是一个链表则是 O(1)

与插入，希尔排序的速度对比

比较代码如下：
 1def insertion_sort(alist):
 2    for index in range(1, len(alist)):
 3        current_value = alist[index]
 4        position = index
 5
 6        while position > 0 and alist[position - 1] > current_value:
 7            alist[position] = alist[position - 1]
 8            position = position - 1
 9
10        alist[position] = current_value
11
12
13def shell_sort(items):
14    length = len(items)
15    gap = 41
16    while gap > 0:
17        for group_start in range(0, gap):
18
19            for index in range(group_start + gap, length, gap):
20                position = index
21                current_value = items[index]
22                while position > group_start and items[position - gap] > current_value:
23                    items[position] = items[position - gap]
24                    position -= gap
25                items[position] = current_value
26
27        gap -= 1
28
29
30def merge_sort(items):
31    if len(items) > 1:
32        middle = len(items) // 2
33        left_half = items[:middle]
34        right_half = items[middle:]
35
36        merge_sort(left_half)
37        merge_sort(right_half)
38
39        left_index = right_index = items_index = 0
40
41        while left_index < len(left_half) and right_index < len(right_half):
42            if left_half[left_index] < right_half[right_index]:
43                items[items_index] = left_half[left_index]
44                left_index += 1
45            else:
46                items[items_index] = right_half[right_index]
47                right_index += 1
48            items_index += 1
49
50        if left_index < len(left_half):
51            items[items_index:] = left_half[left_index:]
52
53        if right_index < len(right_half):
54            items[items_index:] = right_half[right_index:]
55
56
57def quick_sort(array):
58    if len(array) < 2:
59        return array
60
61    index = len(array) // 2
62    pivot = array[index]
63    left = []
64    right = []
65    for item in (array[:index] + array[index + 1:]):
66        if item <= pivot:
67            left.append(item)
68        else:
69            right.append(item)
70
71    return quick_sort(left) + [pivot] + quick_sort(right)
72
73
74from timeit import Timer
75import random
76
77t1 = Timer('insertion_sort(alist1)', 'from __main__ import insertion_sort', globals=globals())
78t2 = Timer('shell_sort(alist2)', 'from __main__ import shell_sort', globals=globals())
79t3 = Timer('merge_sort(alist3)', 'from __main__ import merge_sort', globals=globals())
80t4 = Timer('quick_sort(alist4)', 'from __main__ import quick_sort', globals=globals())
81
82length = 10000
83times = 1
84alist = list(range(length))
85alist1 = list.copy(alist)
86alist2 = list.copy(alist)
87alist3 = list.copy(alist)
88alist4 = list.copy(alist)
89print(t1.timeit(number=times), t2.timeit(number=times), t3.timeit(number=times), t4.timeit(number=times))
90
91alist = random.sample(list(range(length)), length)
92alist1 = list.copy(alist)
93alist2 = list.copy(alist)
94alist3 = list.copy(alist)
95alist4 = list.copy(alist)
96print(t1.timeit(number=times), t2.timeit(number=times), t3.timeit(number=times), t4.timeit(number=times))

结果

排序耗时(秒)有序列表(1K)有序列表(10K)有序列表(100K）无序列表(1K)无序列表(10K)无序列表(100K)
插入排序0.0001784720.0023851710.0238597030.053225515.83567684590.22879396
希尔排序0.006685450.0675835641.0623839980.008936860.26069421716.79080933
归并排序0.0025036690.031031950.3926149320.0034196720.0482902160.737126917
快速排序0.001213110.0147460890.2323926760.0016025810.0197874540.331404756

归并排序在整体表现上还是很不错，它同快速排序都是一样的 O(n log n) 时间复杂度，所以还是有一定资格拿它与快速排序相比较的。从某种意义上讲快速排序是对归并排序的改进

  1. 归并排序是每次对半拆分，快速排序选定基准值进行拆分
  2. 归并排序拆分时不用与基准值的比较，拆分效率高于快速排序
  3. 它们都是要拆分到只剩下单个元素的列表
  4. 归并排序在归并时合并子列表麻烦些，快速排序合并子列表直接串起来 -- 归并排序效率差在这里
  5. 归并排序归并是一次遍历，快速排序在拆分时要一次遍历，所以它们的复杂度都是 O(n log n)

虽然它先要傻傻的把整个列表拆成全是单元素的列表，但归并是处理的都是有序列表，这可省了不少的时间。所以归并排序不在于怎么拆分，关键在于归并的过程上的高效，所以才叫做归并排序。由于它采用折半拆分，也就不能容易造成调用栈溢出的情况，因为 32 的栈深度可以处理 232 = 4294967296 个元素，Python 默认的栈深度 sys.getrecursionlimit() 是 1000。 永久链接 https://yanbin.blog/the-last-basic-merge-sorting/, 来自 隔叶黄莺 Yanbin's Blog
[版权声明] 本文采用 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 进行许可。